metode Newton Raphson

Metode Newton-Raphson merupakan salah satu metode terbuka untuk menentukan solusi akar dari persamaan non linier, dengan prinsip utama sebagai berikut :

1. metode ini melakukan pendekatan terhadap kurva f(x) dengan garis singgung (gradien) pada suatu titik    nilai awal.

2. nilai taksiran selanjutnya adalah titik potong antara garis singgung(gradien) kurva dengan sumbu x 

Metode Newton Rapshon sering digunakan karena kesederhanaannya dan mempunyai konvergensi yang cepat. Karena metode ini merupakan metode Terbuka, maka tetap diperlukan nilai tebakan awal untuk Xo. Secara geometri, metode Newton Raphson hampir sama dengan metode regula falsi, bedanya garis yang dipakai adalah garis singgung. Dengan menggunakan x0 sebagai tebakan awal, dilanjutkan dengan mencari titik (x0, f(x0)). Kemudian dibuat garis singgung dari titik (x0, f(x0)), sehingga diperoleh titik potong (x1, 0) antara sumbu-x dan garis singgung titik (x0, f(x0)). Kemudian dilanjutkan lagi dengan mencari titik (x1, f(x1)). Dari titik (x1, f(x1)) kemudian dibuat garis singgung, sehingga diperoleh titik potong (x2, 0) antara sumbu-x dan garis singgung titik (x1, f(x1)).

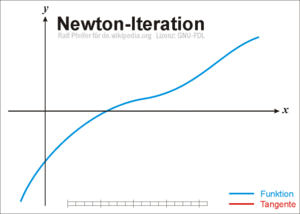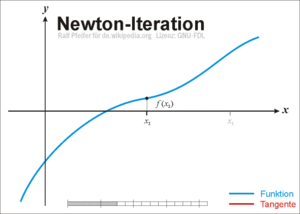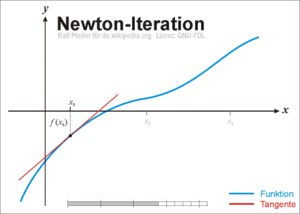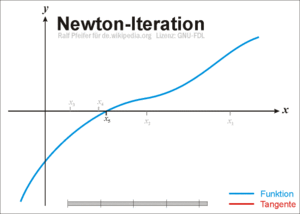
adapun langkah-langkah pengerjaaan metode Newton-Raphson yaitu :

1. definisikan fungsi f(x) dan f'(x)

2. Tentukan toleransi error (e) dan iterasi maksimum (n)
3. Tentukan nilai pendekatan awal x0
4. Hitung f(x0) dan f1(x0)
5. Untuk iterasi I = 1 s/d n atau |f(xi)| ≥ e

6. Akar persamaan adalah nilai xi yang terakhir diperoleh.

Contoh:

Hitung akar f(x)=e^x – 5x^2,

ε = 0.00001

x0 = 0.5

Penyelesaian

Contoh 1:

Hitung akar f(x)=e^x – 5x^2,

ε = 0.00001

x0 = 0.5

Penyelesaian

Sehingga iterasi Newton Raphson nya sebagai berikut:

Hasil setiap iterasi sebagai berikut:

Jadi, hampiran akarnya adalah x=0.605267.

Contoh 2:

Tentukan akar dari persamaan 4x³ – 15x² + 17x – 6 = 0 menggunakan Metode Newton-Raphson.

Penyelesaian :

f(x) = 4x³ – 15x² + 17x – 6

f’(x) = 12x² – 30x + 17

ambil titik awalnya = 3

sehingga hasil perhitungan iterasi Newton Raphson nya disajikan pada tabel sebagai berikut

n	xn	f(xn)	f’(xn)
1 2 3 4 5 6	3 2.48571 2.18342 2.04045 2.00265 2.00001 2.00000	18 5.01019 1.24457 0.21726 0.01334 0.00006 0.00000	35 16.57388 8.70527 5.74778 5.04787 5.00023 5.00000

hasil perhitungan di atas diperoleh dengan cara :

iterasi 1 :

f(3) = 4(3)³ – 15(3)² + 17(3) – 6 = 18

f’(3) = 12(3)² – 30(3) + 17 = 35

x₁ = 3 – 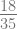 = 2.48571

iterasi 2 :

f(2.48571) = 4(2.48571)³ – 15(2.48571)² + 17(2.48571) – 6 = 5.01019

f’(2.48571) = 12(2.48571)² – 30(2.48571) + 17 = 16.57388

x₂ = 2.48571 – 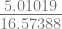 = 2.18342

iterasi 3 :

f(2.18342) = 4(2.18342)³ – 15(2.18342)² + 17(2.18342) – 6 = 1.24457

f’(2.18342) = 12(2.18342)² – 30(2.18342) + 17 = 8.70527

x₃ = 2.18342 – 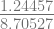 = 2.04045

iterasi 4 :

f(2.04045) = 4(2.04045)³ – 15(2.04045)² + 17(2.04045) – 6 = 0.21726

f’(2.04045) = 12(2.04045)² – 30(2.04045) + 17 = 5.74778

x₄ = 2.04045 – 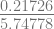 = 2.00265

iterasi 5 :

f(3) = 4(2.00265)³ – 15(2.00265)² + 17(2.00265) – 6 = 0.01334

f’(2.00265) = 12(2.00265)² – 30(2.00265) + 17 = 5.04787

x₅ = 2.00265 – 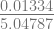 = 2.00001

iterasi 6 :

f(2.00001) = 4(2.00001)³ – 15(2.00001)² + 17(2.00001) – 6 = 0.00006

f’(2.00001) = 12(2.00001)² – 30(2.00001) + 17 = 5.00023

x₆ = 2.00001 – 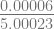 = 2.00000

iterasi 7 :

f(2) = 4(2)³ – 15(2)² + 17(2) – 6 = 0

Judul: metode Newton Raphson; Ditulis oleh Unknown; Rating Blog: 5 dari 5